CV

Online Adaptive ICCBF

PaperTitle
Learning to Refine Input Constrained Control Barrier Functions via Uncertainty-Aware Online Parameter Adaptation
Author
Taekyung Kim, Robin Inho Kee, and Dimitra Panagou
Affiliation
Department of Robotics, University of Michigan
Venue
2 more properties
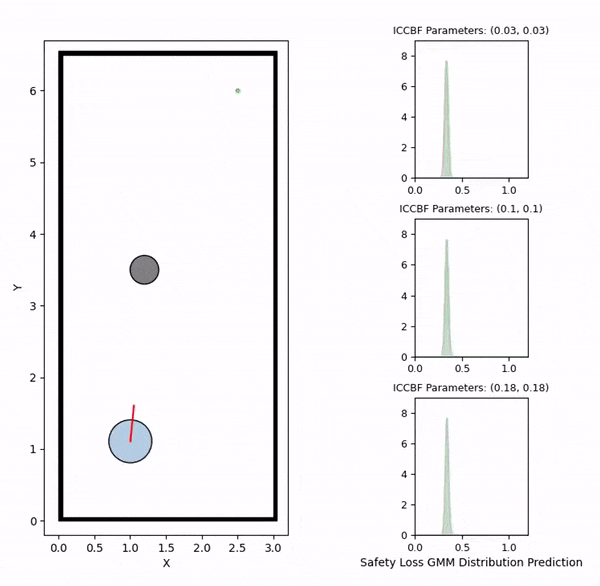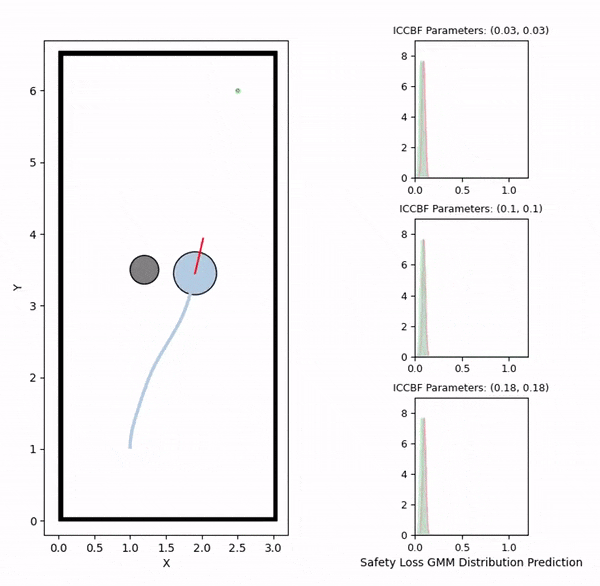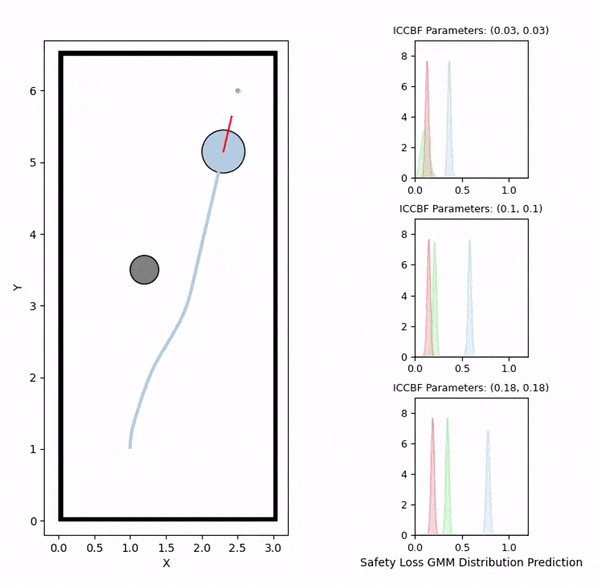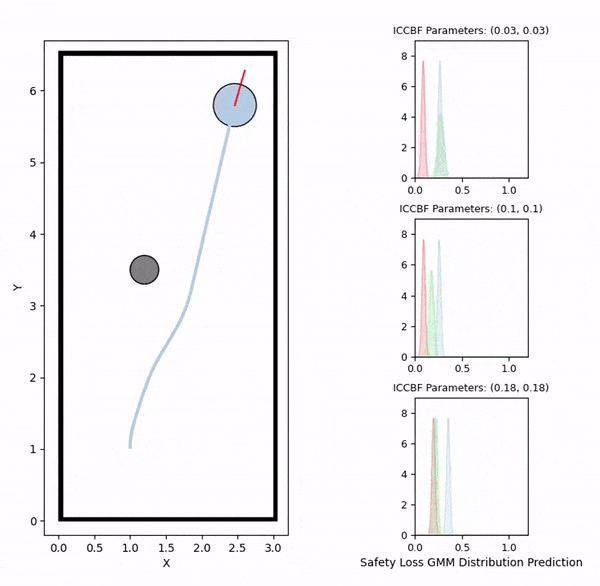
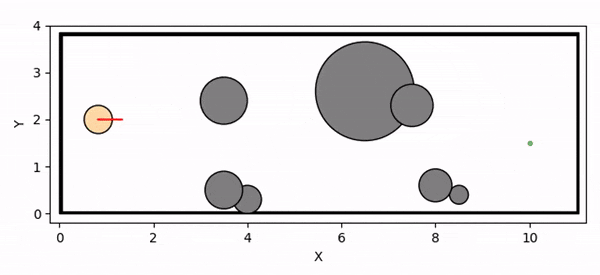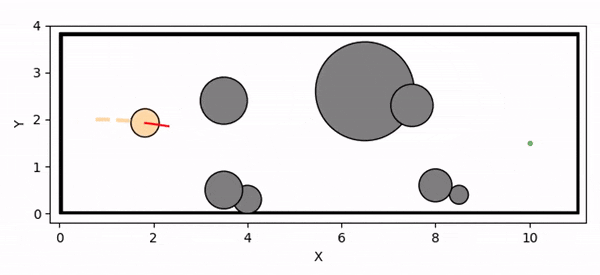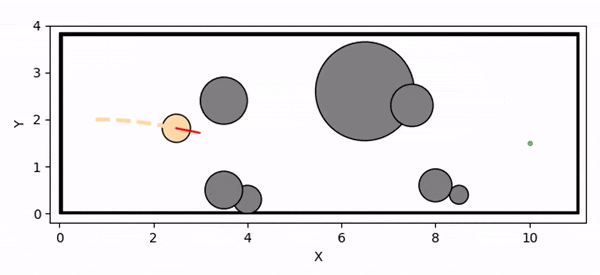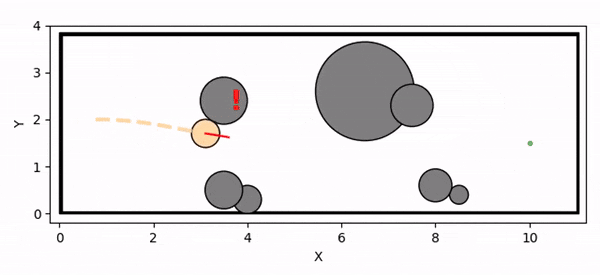
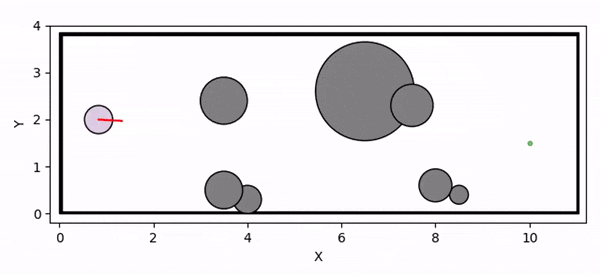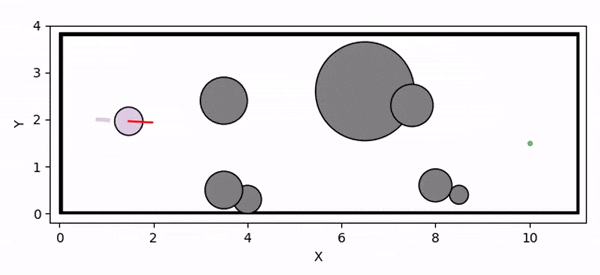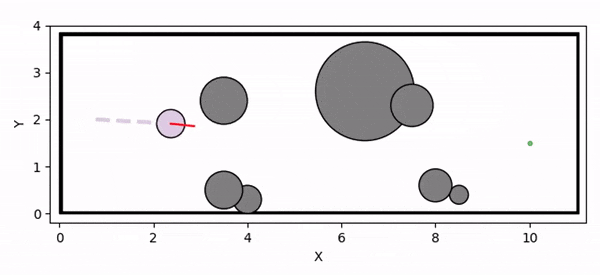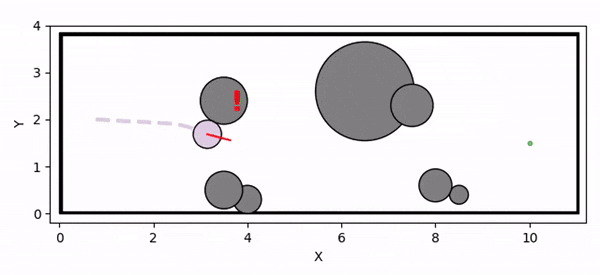
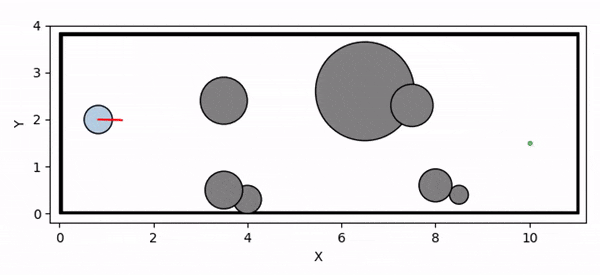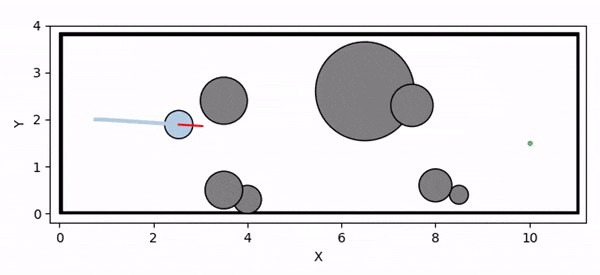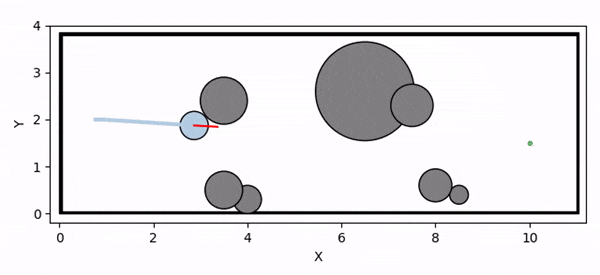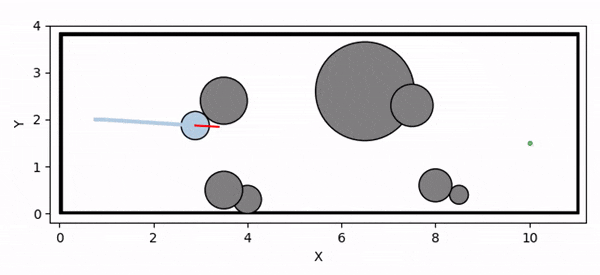
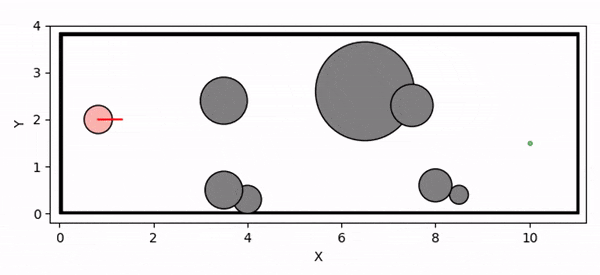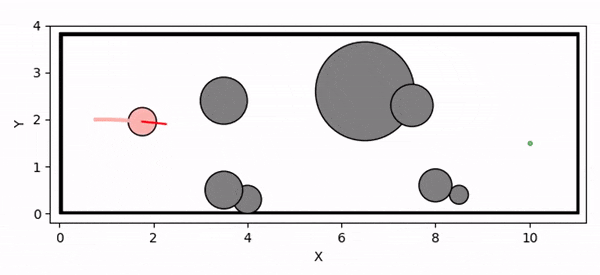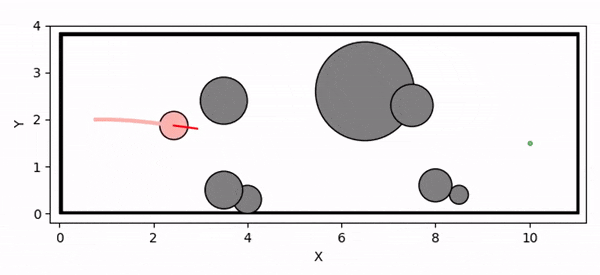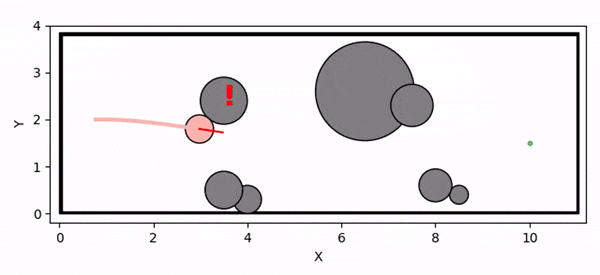
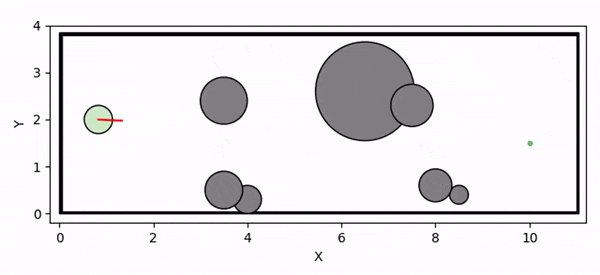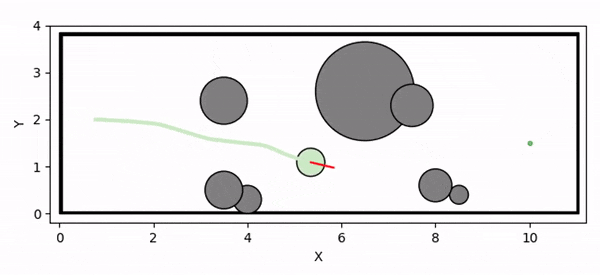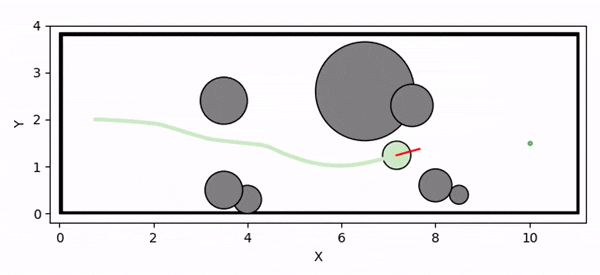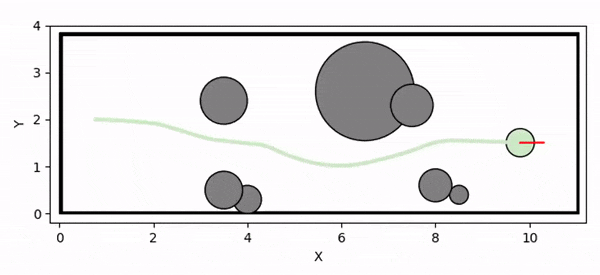
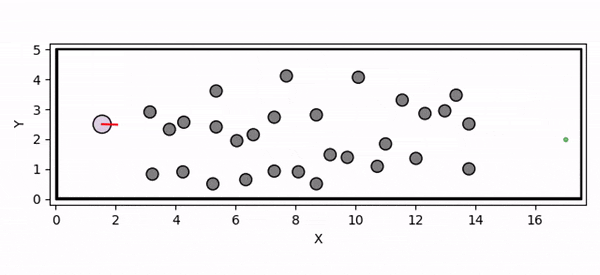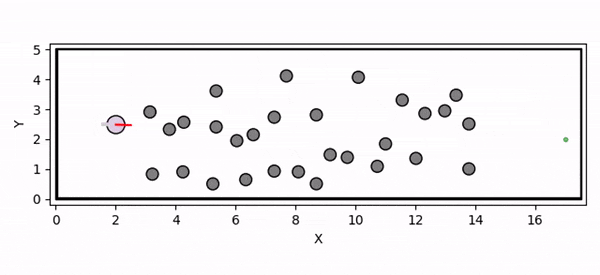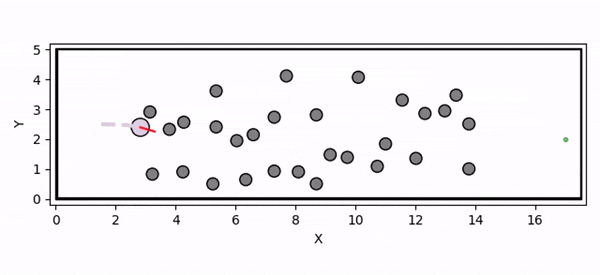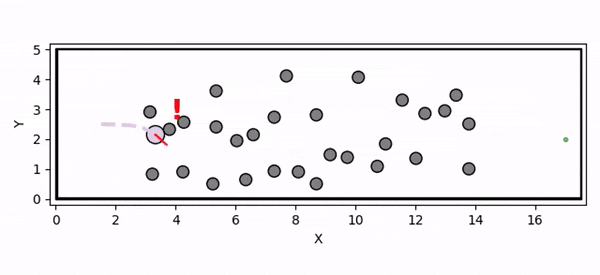
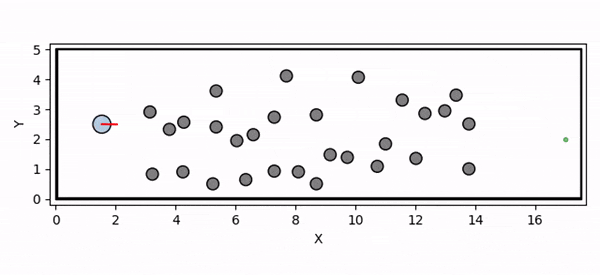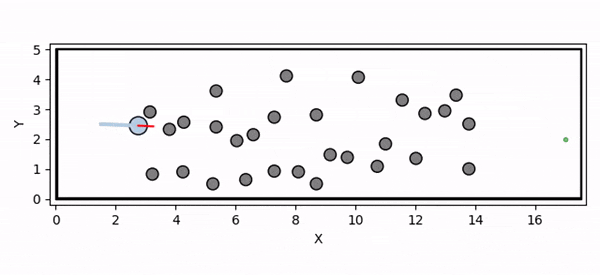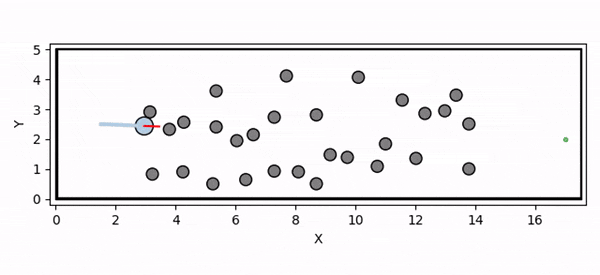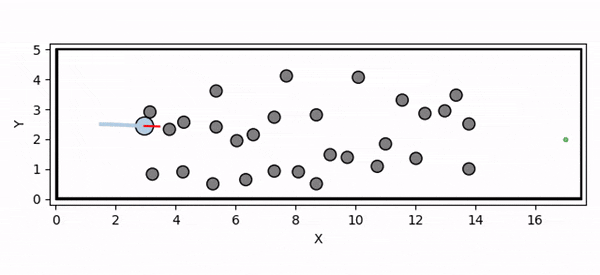
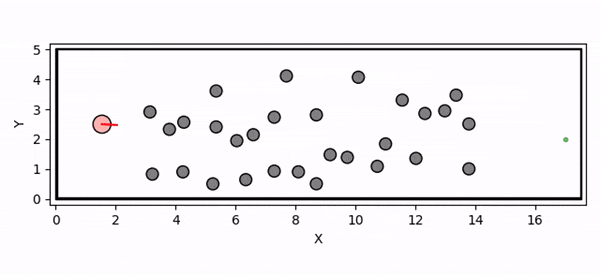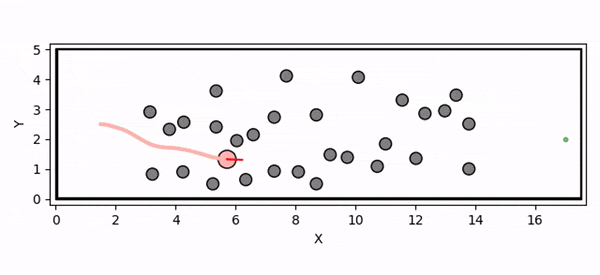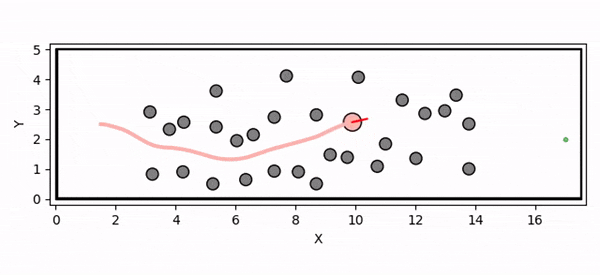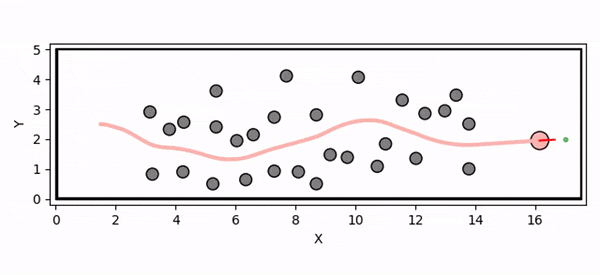
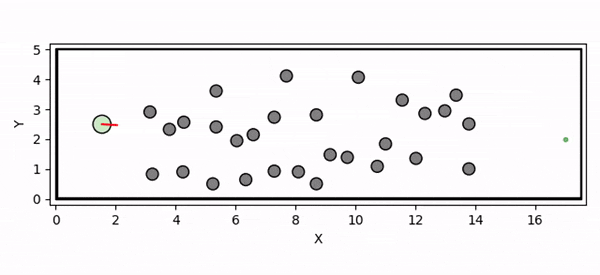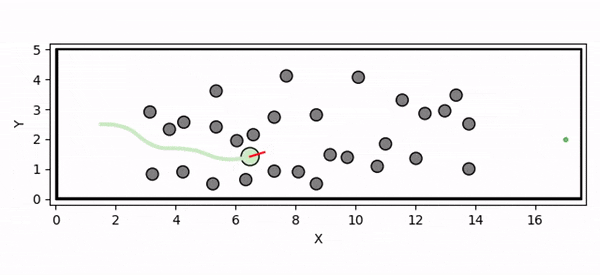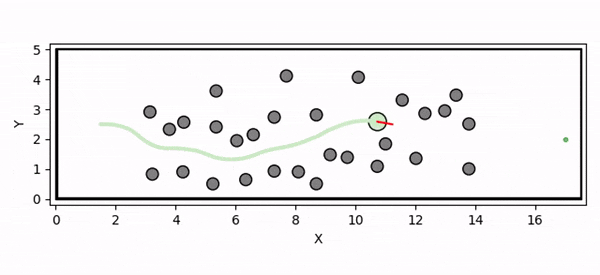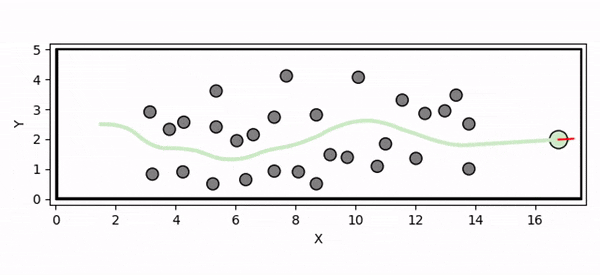
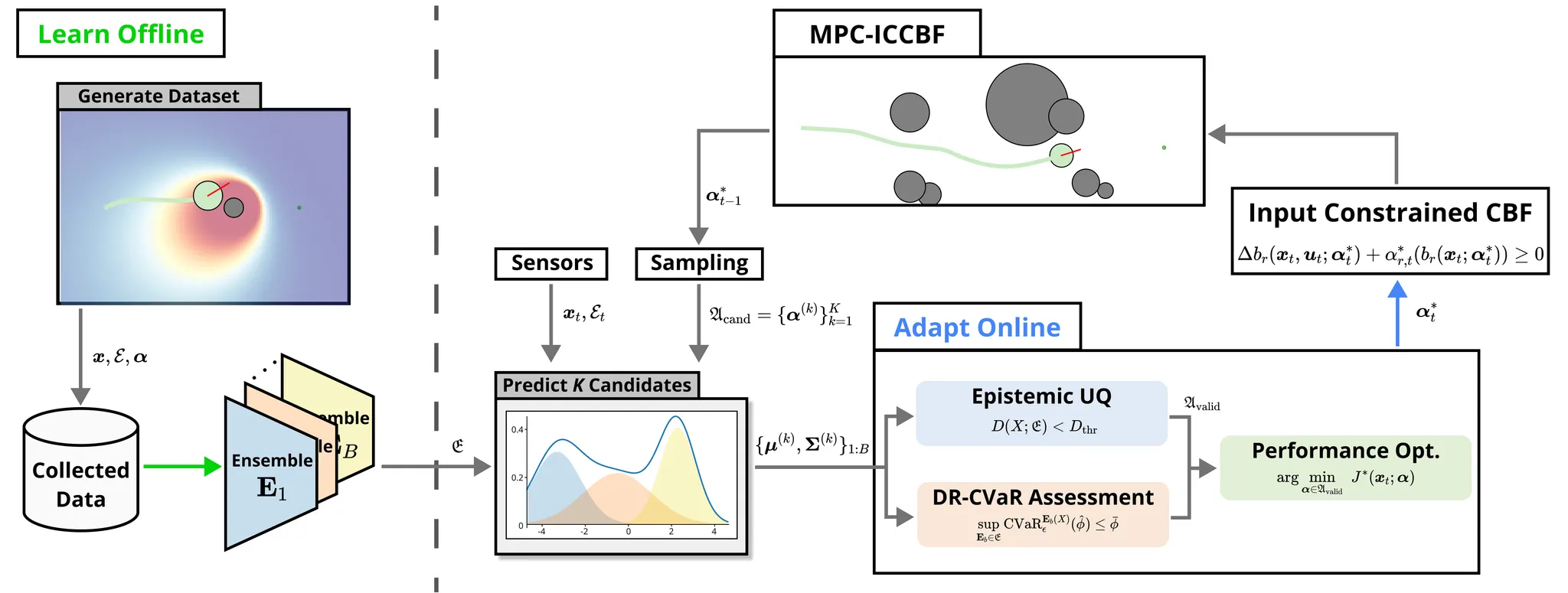
Overview diagram of the Online Adaptive ICCBF algorithm applied to MPC framework.
The Online Adaptive ICCBF algorithm dynamically adapts Input Constrained Control Barrier Function (ICCBF) parameters to optimize performance while ensuring safety for input-constrained nonlinear systems. Our approach leverages a Probabilistic Ensemble Neural Network (PENN) to predict performance and risk metrics, considering both epistemic and aleatoric uncertainties. The algorithm incorporates a two-step verification process using Jensen-Rényi Divergence (JRD) and Distributionally-Robust Conditional Value at Risk (DR-CVaR) to identify valid parameters. By adapting ICCBF parameters online based on the current state and nearby environment, our method optimizes performance while maintaining safety.

Motivation

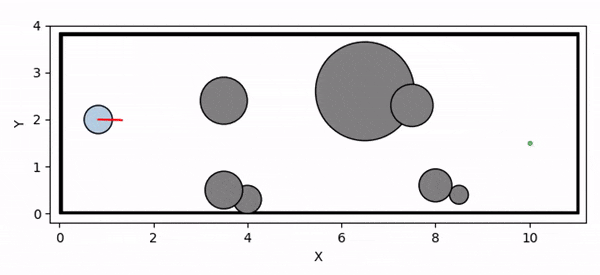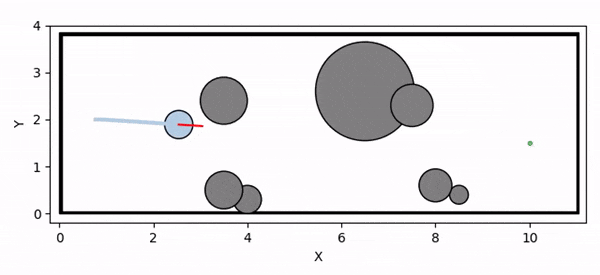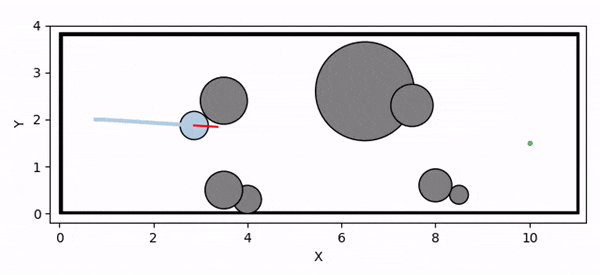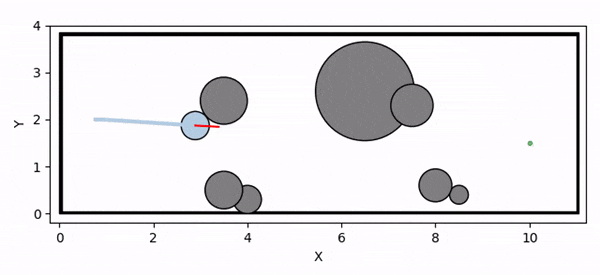
Deadlock occurs due to overly conservative CBF constraint
Controller infeasibility under input constraints leads to collision with the obstacle
Control Barrier Functions (CBFs) are widely used in robotics to ensure system safety. However, finding valid CBFs that guarantee persistent safety and feasibility remains an open challenge, especially in systems with input constraints. Traditional approaches often rely on manually tuning the parameters of the class K functions for the CBF conditions a priori. The performance of CBF-based controllers is highly sensitive to these fixed parameters, potentially leading to overly conservative behavior (such as deadlock) or safety violations (due to infeasibility).

Algorithm Breakdown

Data Generation

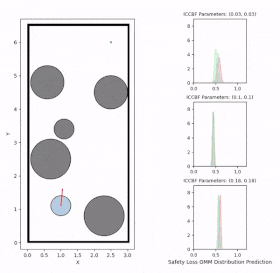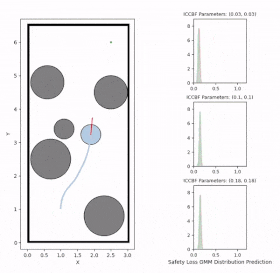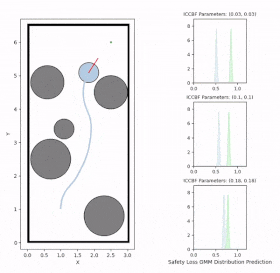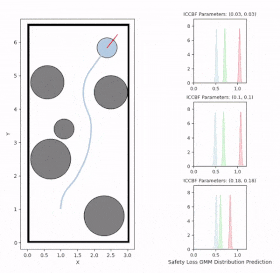
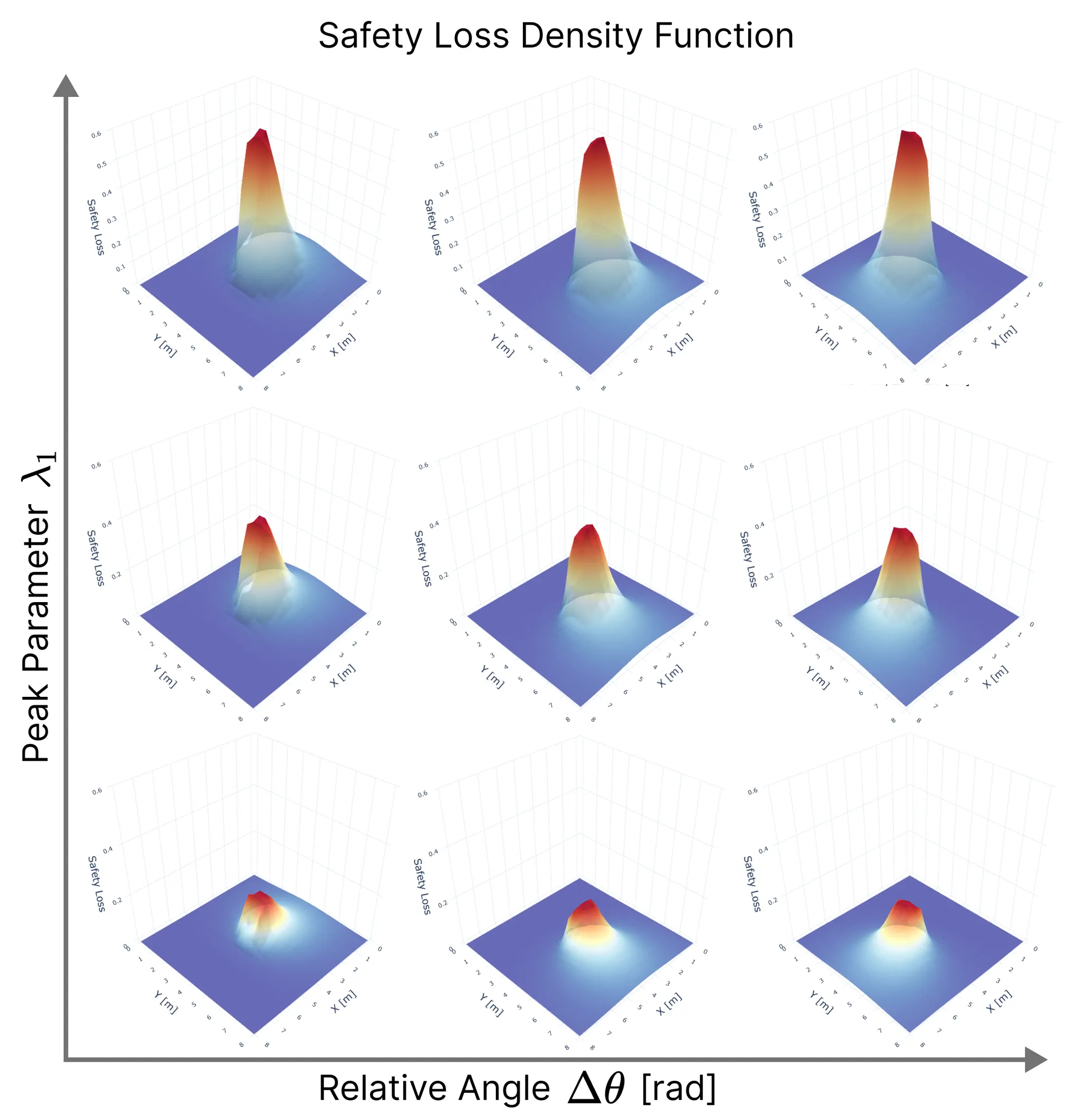
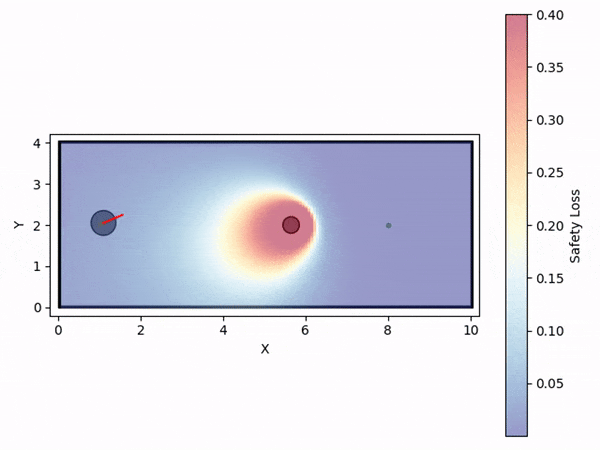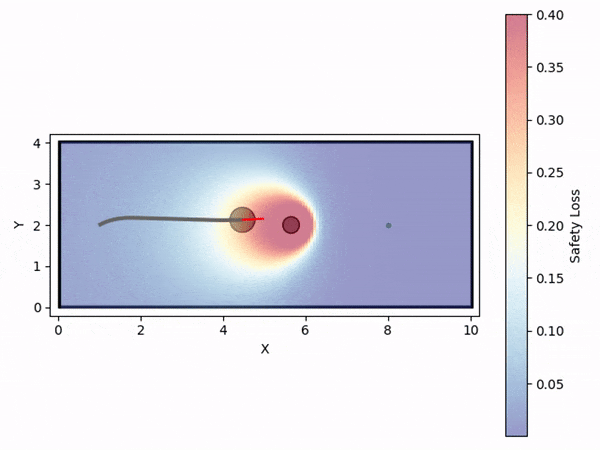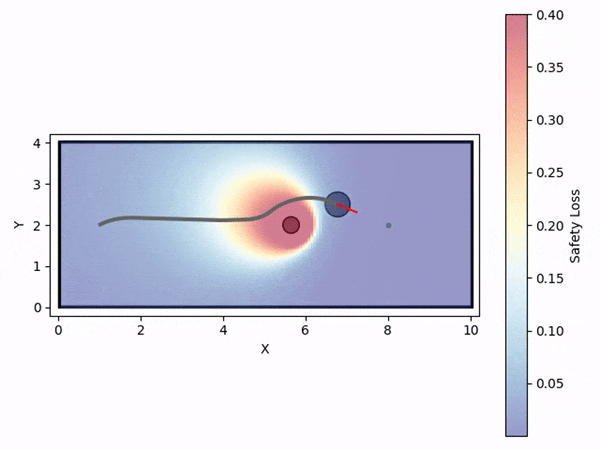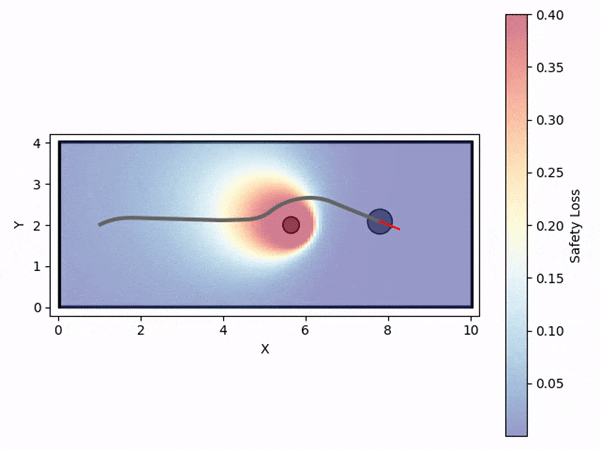
Safety loss density function
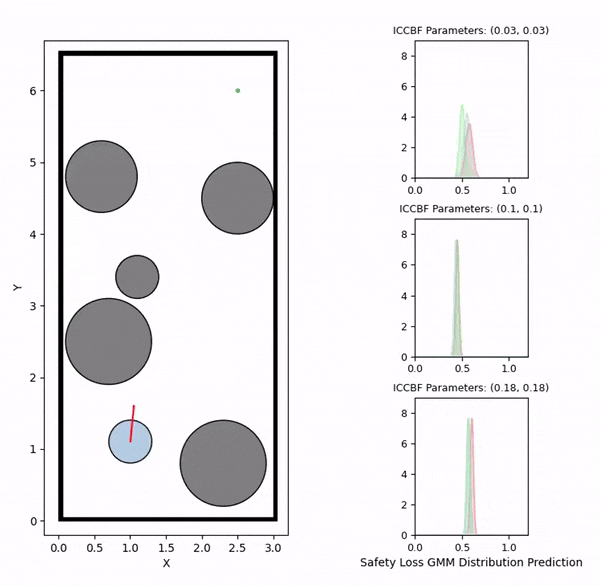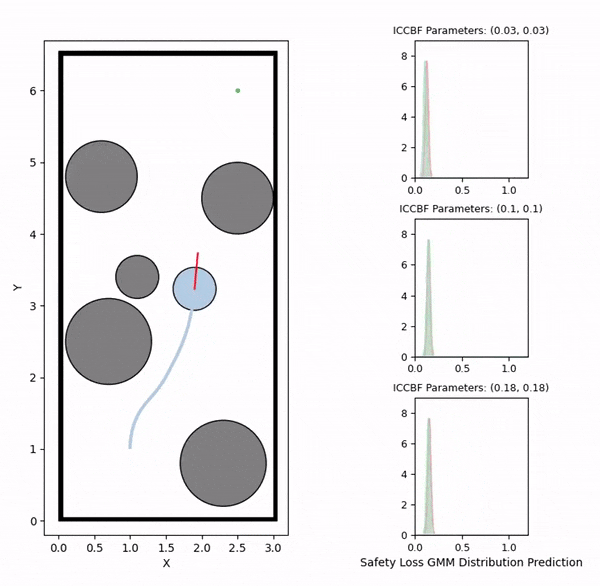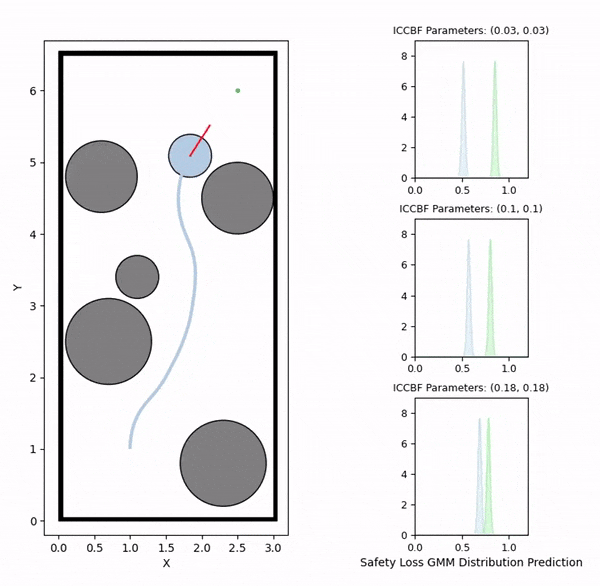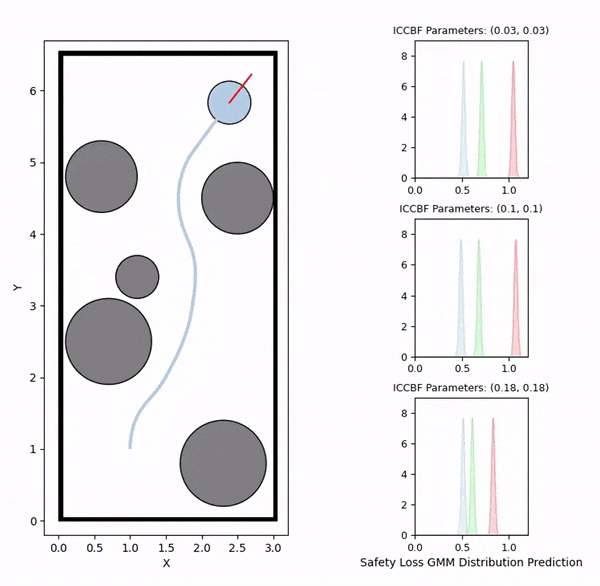
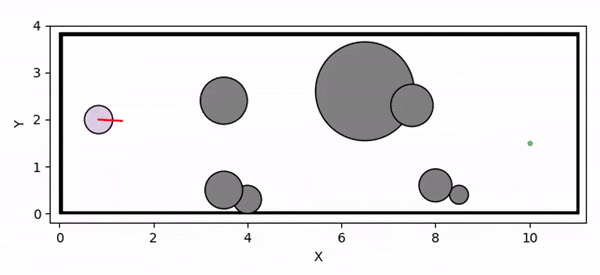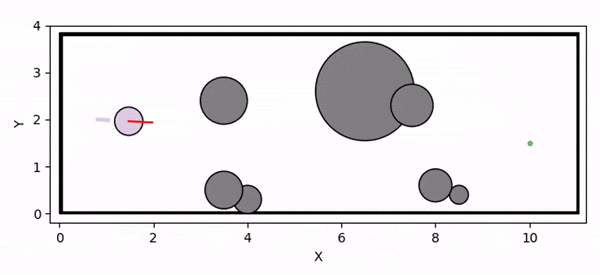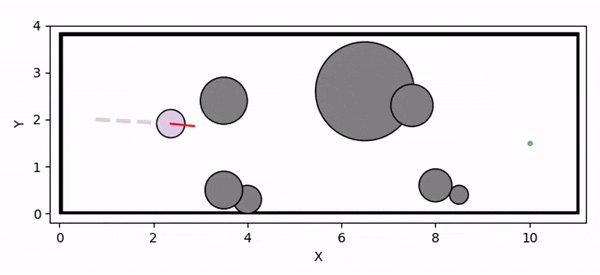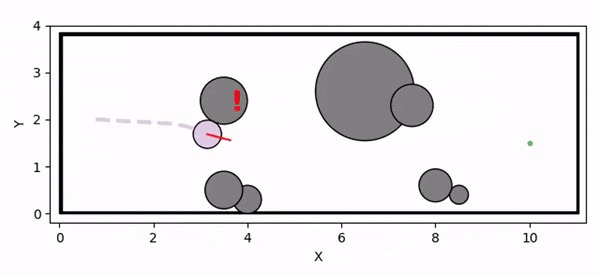
Data generation example (visualizing safety loss)
We initially generate robot trajectories using the CBF-based controller to form the training dataset by varying the robot's initial state, obstacle configurations, and class-K function parameters. The risk level and deadlock time are recorded as the ground truth for prediction. The risk level is computed as the maximum safety loss value during navigation, defined by a safety loss density function that captures the collision risk.

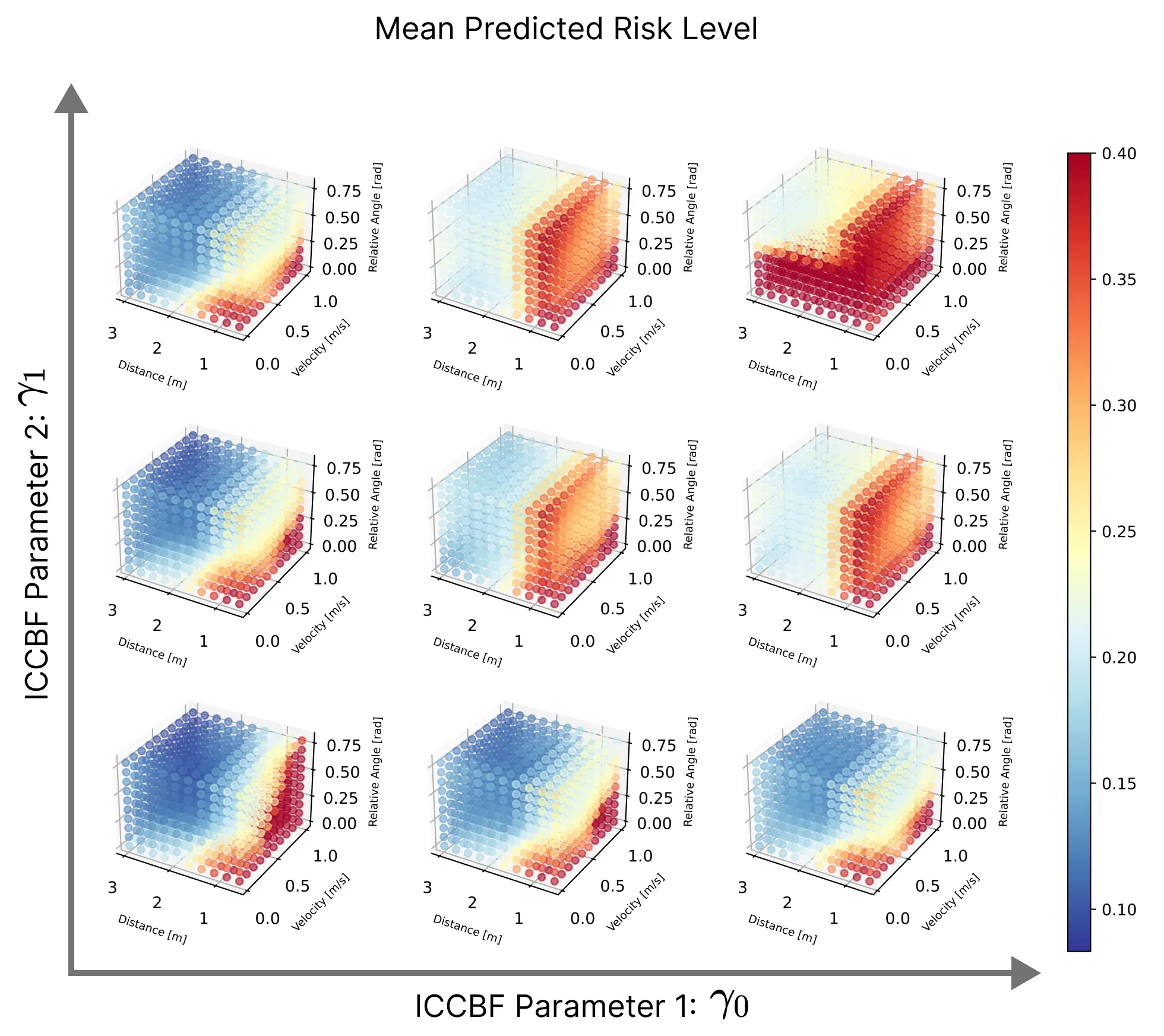
PENN Model Prediction

Visualization of the mean predicted risk level from varying inputs
We train the PENN model on the dataset, observing that the predicted risk level increases with higher CBF parameters, closer distances to obstacles, higher velocities, and smaller relative angles to obstacles.
Given the PENN model’s nature, the predicted values follow a Gaussian Mixture Model. We implement a two-step verification process using this PENN model to predict the CBF class K functions of interest. First, we quantify epistemic uncertainty using a closed-form solution from Jensen-Rényi Divergence (JRD) and discard predictions with low confidence. Next, we apply Distributionally-Robust Conditional Value at Risk (DR-CVaR) to ensure probabilistic satisfaction of the ICCBF validity condition. Further details on the relationship between the predicted risk level and the ICCBF validity can be found in the paper.
Distributionally Robust CVaR

Visualize Prediction Results for CBF Parameters of Interest

The visualizations above show the predicted risk levels online, without adapting the parameters. We illustrate three candidate ICCBF parameter sets — low, medium, and high. They reveal the same patterns with our offline predictions, showing increased risk levels as the robot moving towards obstacles. Additionally, you can observe instances of high disagreement between ensemble models, indicating low confidence in those predictions, which are subsequently discarded.
Once valid ICCBF parameter sets are identified, we optimize the controller's performance by selecting the parameters with the minimum predicted deadlock time. By repeating this process at each time step, it continuously refines the ICCBF parameters based on the current state and the predictions from the PENN model, thereby optimizing performance while maintaining safety.

Preview Experiments

Scenario 1

MPC-CBF w/ Low Parameters
MPC-CBF w/ High Parameters
Optimal Decay CBF-QP
Optimal Decay MPC-CBF
Online Adaptive ICCBF w/ MPC (Ours)
The video demonstrates simulation results comparing five different methods.

Scenario 2

MPC-CBF w/ Low Parameters *
MPC-CBF w/ High Parameters
Optimal Decay CBF-QP
Optimal Decay MPC-CBF
Online Adaptive ICCBF w/ MPC (Ours)
For more details on the experiments and implementation, please visit our GitHub repository.
(*Note: MPC-CBF with low parameters becomes infeasible at the early stage in this experiment, but we simulate it until collision.)

Acknowledgement

This work has been supported by the National Science Foundation (NSF) through Award No. 1942907. I also would like to thank Rahul H. Kumar for collaboration on the hardware experiments.

BibTex

@inproceedings{kim2024learning, author = {Taekyung Kim and Robin Inho Kee and Dimitra Panagou}, title = {Learning to Refine Input Constrained Control Barrier Functions via Uncertainty-Aware Online Parameter Adaptation}, booktitle = {{arXiv} preprint {arXiv}:2409.14616}, shorttitle = {Online-Adaptive-CBF}, year = {2024} }
LaTeX
복사