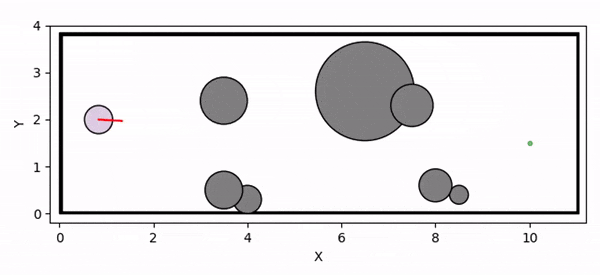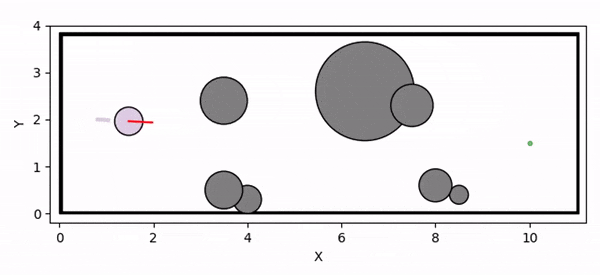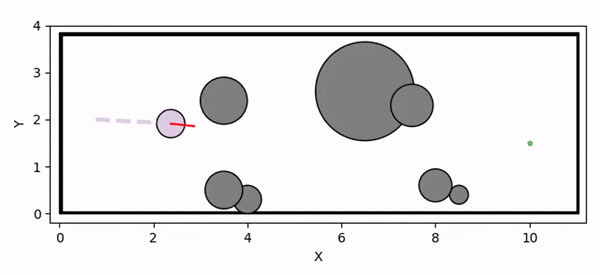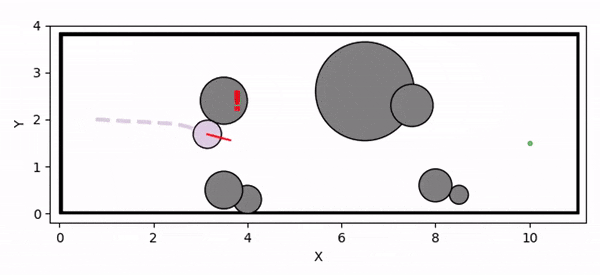
Conceptual illustration of the inner safe set and locally validated CBF parameter.
We present a novel theoretical framework for online adaptation of Control Barrier Function (CBF) parameters, i.e., the class K functions, under input constraints. To this end, we propose the concept of locally validated CBF parameters, where adapting these parameters ensures that the system trajectories remain safe within the finite horizon. (a) A candidate inner safe set defined via an Input Constrained CBF cannot be rendered forward invariant using the given CBF parameter. (b) With locally validated CBF parameters, the trajectory remains within the inner safe set over the finite horizon, ensuring safety for that interval. By adapting the CBF parameters, the corresponding inner safe set is reshaped dynamically, alleviating conservatism by allowing the trajectory to extend beyond a fixed, globally verified inner safe set.
.png&blockId=1ca18d5c-31e3-816b-b2ae-f17349bcaa27)
.png&blockId=1ca18d5c-31e3-8184-9ba4-e43e96b1548c)
Motivation
Deadlock occurs due to overly conservative CBF constraint
Controller infeasibility under input constraints leads to collision with the obstacle
Control Barrier Functions (CBFs) are widely used in robotics to ensure system safety. However, finding the CBF parameters (class K functions) is particularly challenging for highly nonlinear and complex systems and becomes even more difficult when input constraints are present. Traditional approaches often rely on manually tuning the parameters of the class K functions for the CBF conditions a priori. The performance of CBF-based controllers is highly sensitive to these fixed parameters, potentially leading to overly conservative behavior (such as deadlock) or safety violations (due to infeasibility).
How to Predict Locally Validated CBF Parameters?
Neural network configurations for CBF parameter adaptation
To adapt CBF parameters online, (a) prior works employ deterministic neural networks that directly output the optimal CBF parameter; however, these approaches do not account for the inherent uncertainty in the predictions, which may lead to catastrophic failures when facing out-of-distribution inputs. (b) In contrast, we propose a probabilistic verification method that, instead of outputting a single set of CBF parameters, takes a candidate set and predicts the distributions of the safety and performance characteristics. This key novelty enables rigorous verification of locally validated CBF parameters despite neural network uncertainty.
Preview Experiments
.png&blockId=1cb18d5c-31e3-8036-acc1-dc51c8b9e3ca)
Illustration of a VTOL quadplane aircraft
We apply our method to a VTOL quadplane transition and landing scenario, where it is the first application of CBFs to VTOL quadplane control tasks.
MPC-CBF w/ low CBF parameters - a significant altitude detour
MPC-CBF w/ high CBF parameters - become infeasible, eventually collide
The videos demonstrate simulation results comparing two baseline methods.
Ours: MPC-CBF w/ CBF parameter adaptation
A closer look
Evolution of the adapted CBF parameters over time.
Our method dynamically adjusts the CBF parameters based on the aircraft’s speed and position. Initially, due to the high speed, it maintains low CBF parameters, prompting the elevator to pitch up and generate additional drag. As the aircraft slows down, the parameters increase to enhance performance.
Acknowledgement
This work has been supported by the Center for Autonomous Air Mobility and Sensing (CAAMS), an NSF IUCRC, under Award Number 2137195. I also would like to thank Daniel Cherenson for valuable discussion on this work.
BibTex
@inproceedings{kim2025how,
author = {Kim, Taekyung and Beard, Randal W. and Panagou, Dimitra},
title = {How to Adapt Control Barrier Functions? A Learning-Based Approach with Applications to a VTOL Quadplane},
booktitle = {},
shorttitle = {How to Adapt Control Barrier Functions},
year = {2025}
}
LaTeX
복사